Steganography is the process if sharing information in an undetectable way. Encryption makes sure your secret can only be understood by the right person. Steganography makes sure nobody else can even tell you are sharing a secret.
using Java WebStart
During the height of the Greek empire messages were tattooed on the heads of servants who were sent off after the hair had grown back. They were given a scroll containing an uninteresting message to deliver while the real message was hidden under their hair. Computers allow the transmission of secret messages without requiring permanent body modification or bad hair cuts. In general steganography is a message which appears to be something else. The best applications of steganography will distribute the information to many people with only one or two of those people knowing how to look for the secret message. This makes it very difficult to determine whom the message was meant for.
This application encodes messages in images which have been subtly changed to hold them. These images are imperceptibly different from the original. For example, if Alice wants to send Bob a message she could just send him an email. If she wants to make sure that Eve (an eavesdropper) can’t read the message then she could encrypt her email. However, even if the message is encrypted Eve will still know that Alice sent Bob a message. Alice could use this program to encode her message in an image. She could then post this image to a free web site like Flickr.com. This image can be viewed by Eve and will look like any normal image. Bob could then use this application to extract the message from the image. For added security Alice could encode an encrypted message in the image.
This sample is a Java client application written using Java Swing. This sample should run on Windows, Linux, MacOS, and any other platform where Java is available. This application requires a Java Development Kit version 1.5 or greater. If you don’t have a copy of the JDK you can download it from http://www.javasoft.com.
The code in this application is free and is released under the Apache 2.0 license. That means you are welcome to use, copy, and change this code as much as you would like. If you find any bugs, have any comments, or make any improvements I would love to hear from you. Other programs are needed to run this application. They are all free, but some of them use different licenses. You should make sure to read and understand each license before using a tool.
Setup
source code
Get the Source Code
You should start by downloading the source code for this sample. It can be found here. Once you have downloaded it you should unzip it to a work directory on your computer.
Get Other Programs
This program has been setup to be built using Apache Ant. Ant is a very popular tool for building Java projects. Building this project without Ant is possible, but it can be tricky to set up. If you don’t have Ant already you should download and install it.
Build and Run
Once you have installed Ant you can build and run the sample application by following these steps:
- Unzip the samples archive to a directory on your machine.
- Open a command prompt and change directories to the location you unzipped the sample to.
- Execute the command
ant(you may need to provide the full path to your Ant installation). - Execute the command
java -jar dist/stegtest.jarto run the sample.
This application comes with a sample image (lily.jpg), but it should work with any JPEG, GIF, PNG or other common image file format. You can open an image once the program has started, or you can pass a the path to an image to the program as a command line argument. Once you have created a second image with your message encoded in it you can save the new image and decode the message at a later time.
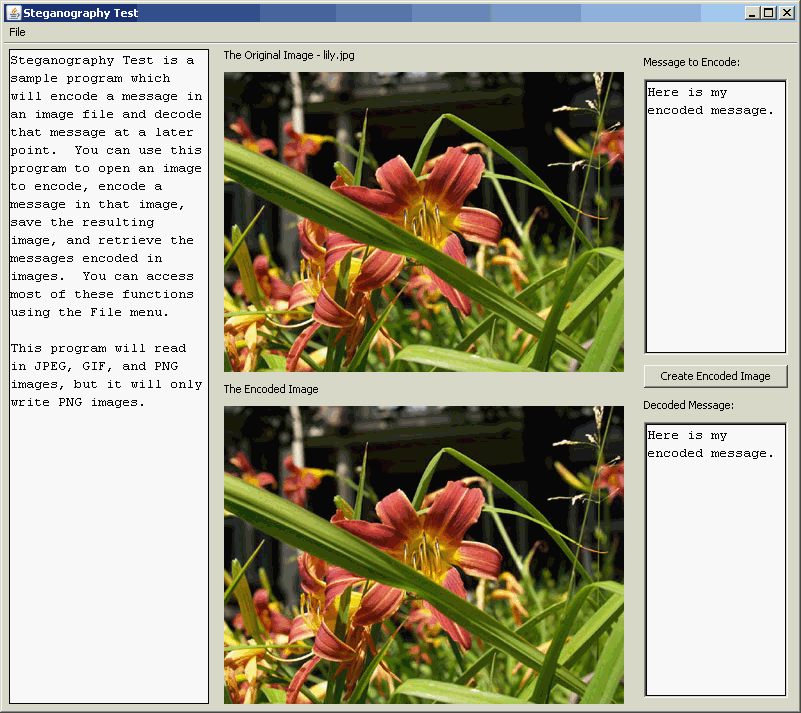
Core Technologies
This program will use the following core technologies:
- Java Swing
- Java 2D API
- Binary Arithmetic
This sample is a Java Swing application. It uses the Java 2D API for loading and manipulating the image. This sample also uses more binary arithmetic than most Java programs. Programmers who do not recognize the >> operator in Java will learn a lot from this sample.
How It Works
This application will make subtle changes to a picture and use those change to encode information. To understand this process it is important to understand the basics of computer graphics storage. Computer images are made up of a set of pixels. Each pixel is a small square of color with a red, green, and blue (RGB) value. Each RGB value can go from 0 to 255. The combination of these three values make up the color of the pixel. For example, an RGB value of 255, 0, 0 would be bright red and an RGB value of 255, 255, 255 would be plain white.
Each of these pixels contains a set of color information which is one byte long. A byte is a collection of eight values of 0 or 1 which are called bits. There are 8 bits to a byte and 4 bits to a nibble. This application will make small changes to the color values of the pixels in an image to encode information. Let’s look at an example:

This is the image lily.jpg with the message “Here is my secret message” encoded in it. I have changed the pixels used to encode the message to be bright blue so they are easy to see. Let’s look at the encoded image without the pixel highlighting:

It is virtually impossible to detect the changes to the pixels in the encoded image. This encoding takes advantage of the human eye’s inability to differentiate subtle color variations. To encode a message it must first be broken down into a set of bytes (one for each character of the message). Each character is stored in 8 bits and those bits are encoded two at a time into each pixel’s RGB value. The program does not change every pixel and starts making changes well after the start of the image so the change will be less easily detected.
Let’s Look at the Code
The code for this application is made up of two files StegTest.java and Actions.java. StegTest.java contains most of the interesting code while Actions.java only contains the code to build the File menu. This article will look at slightly simplified versions of the encoding and decoding algorithms. The code for loading, saving, and deconstructing the image can be found in the sample code archive along with a lot more code comments.
StegTest.java
StegTest.java is a Java class which extends JPanel and implements ActionListener. Extending JPanel means that this class will be a component in the UI. This class also handles the encoding and decoding of messages, the creation of the application’s frame, and the loading and saving of images. Let’s start by looking at a simplified version of the encodeMessage method.
private static int[][][] encodeMessage(int[][][] origData, int cols, int rows, String msg)
{
int[][][] imgData = new int[rows][cols][4];1
for (int row = 0;row < rows;row++) {
for (int col = 0;col < cols;col++) {
imgData[row][col][0] = origData[row][col][0];
imgData[row][col][1] = origData[row][col][1];
imgData[row][col][2] = origData[row][col][2];
imgData[row][col][3] = origData[row][col][3];
}
}
byte[] msgBytes = null;
msgBytes = msg.getBytes("ISO-8859-1");2
if ((msgBytes.length + 1 % 3 != 0)) {3
int toAdd = (3 - (msgBytes.length % 3)) - 1;
byte tmpBytes[] = new byte[msgBytes.length + toAdd];
for (int i = 0; i < toAdd; i++) {
tmpBytes[msgBytes.length + i] = (byte)'!';
}
System.arraycopy(msgBytes, 0, tmpBytes, 0, msgBytes.length);
msgBytes = tmpBytes;
}
byte tmpBytes[] = new byte[msgBytes.length + 4];4
tmpBytes[0] = '~';
tmpBytes[1] = '~';
tmpBytes[2] = '~';
tmpBytes[msgBytes.length + 3] = (byte)'!';
System.arraycopy(msgBytes, 0, tmpBytes, 3, msgBytes.length);
msgBytes = tmpBytes;
byte[] twoBitData = new byte[4 * msgBytes.length];5
int twoBitCount = 0;
for (byte element:msgBytes) {
twoBitData[twoBitCount++] = (byte) (element & LSB_MASK_READ);6
twoBitData[twoBitCount++] = (byte) ((element >> 2) & LSB_MASK_READ);
twoBitData[twoBitCount++] = (byte) ((element >> 4) & LSB_MASK_READ);
twoBitData[twoBitCount++] = (byte) ((element >> 6) & LSB_MASK_READ);
}
int skipCount = 0;
twoBitCount = 0;
for (int row = 0; row < rows; row++) {
for (int col = 0; col < cols; col++) {
if ((row * col > INSERTIONPOINT) &&
(twoBitCount < twoBitData.length) &&
skipCount-- == 0) {
imgData[row][col][1] = (imgData[row][col][1] & LSB_MASK_WRITE) |
twoBitData[twoBitCount++];6
imgData[row][col][2] = (imgData[row][col][2] & LSB_MASK_WRITE) |
twoBitData[twoBitCount++];
imgData[row][col][3] = (imgData[row][col][3] & LSB_MASK_WRITE) |
twoBitData[twoBitCount++];
skipCount = twoBitData[twoBitCount - 1];7
}
}
}
return imgData;9
}
|
The encodeMessage method takes the data of the image and a message to encode and returns a new set of image data containing the encoded message. It is important that this method copies the image 1 before making any changes to avoid changing the original image. The next step is to get the bytes of the message 2. We want the bytes of the message in the ISO-8859-1 encoding otherwise known as Latin-1 or ASCII. There will be more discussion about encodings later.
Each character is represented as four pairs of two bits each. However, each pixel can only hold three pairs of two bits each (one for the red, one for the blue, and one for the green color values). That means three characters will be stored evenly in four pixels. In order to make this math work well we will pad out our message until it has a length of characters evenly divisible by three 3. Once we have done that we also want to surround the message with some special characters 4. The message will begin with three tildes so we can identify it later and it will end with an exclamation point so we know when to stop reading the string. It is worth noting that we are using the byte value of these characters which is a different number from the character value. That allows users to still use these characters in their encoded message.
Now that we have ensured our string is the correct length we want to break it up into two bit pairs. These pairs will be held in an array so we can add those values to the pixel data later 5. Each character will create four two bit pairs so we need to make sure our array is four times larger then our message. We will then use a bit mask 6 to separate the values of each byte. If the byte had a value of 01001000 then the first value in the array would be 01, the second value would be 00, the third value would be 10 and the fourth value would be 00. 01001000 is the binary code for the capital H which starts our message.
Once the message has been broken into bit pairs we must encode that data in each pixel. We do this by replacing the two least significant bits with new values 7. The least significant bits are the ones which can be changed while making the smallest impact on the number. For example, replacing the two least significant bits of the value 11010010 with 01 will result in the number 11010001. This is the same as changing the number 210 to 209.
Once we have updated the RGB values for a pixel we will determine how many pixels to skip before changing the next pixel 8. It is important that we don’t change the pixels all together since this would be more visible when viewing the image. We will use one of the values we are writing to determine the amount we skip. We will determine which pixel to change first by using a constant value. You could add a little more security to this sample by requiring the user to choose and then remember the initial pixel to change.
At this point we have created a new image with slightly changed pixel values. The last step is to return 9 that data to the caller of this method. It is important to realize that this is the pixel color data for the new image, but it is not an image. This data must be converted back into a one dimensional array and parsed into an image by the caller of this method
Encoding the message is just half of the process. We also must be able to decode the message. This process begins with the getMessage method. This method must perform the reverse of the encodeMessage method. It is also worth noting that this method can not recreate the original image. Encoding the message in the original message is an information losing operation since the original color values of the changed pixels are not saved.
Unlike the encodeMessage method the getMessage method is broken into two parts. The getMessage method is responsible for reconstituting the bits from the pixel data and the decodeString method is responsible for recombining those bits into valid characters. Let’s start by taking a look at a simplified version of the getMessage method.
private static String getMessage(int[][][] data, int cols, int rows)
{
int skipCount = 0;1
int twoBitCount = 0;
m_startCharCount = 0;
m_foundTerminator = false;2
byte[] twoBitData = new byte[(rows * cols - INSERTIONPOINT) * 3];3
int byteCount = 0;
StringBuffer message = new StringBuffer();
for (int row=0; row < rows; row++) {
for (int col=0; col < cols; col++) {
if ((row * col > INSERTIONPOINT) && (skipCount-- == 0)) {
twoBitData[twoBitCount++] = (byte) (data[row][col][1] & LSB_MASK_READ);4
twoBitData[twoBitCount++] = (byte) (data[row][col][2] & LSB_MASK_READ);
twoBitData[twoBitCount++] = (byte) (data[row][col][3] & LSB_MASK_READ);
byteCount += 3;
skipCount = twoBitData[twoBitCount - 1];5
if ((byteCount % BUFFER_LENGTH) == 0) {6
message.append(decodeString(twoBitData,
twoBitCount - BUFFER_LENGTH, twoBitCount));
if (m_foundTerminator) {7
return message.toString();
}
}
}
}
}
return null;
}
|
When getting the message we need to make sure we perform the operation exactly the opposite of the way we encoded the message. If this method gets the pixel count wrong the bits will be off and not produce a valid message. This method will need to skip 1 pixels based on the values of the message bits. In addition to reading out the message this method has the added responsibility of knowing when to stop reading values 2. This method will look for the terminator character we used when encoding the message (the byte value of !) to know when to stop reading the message.
The first step is to initialize the array which will hold the bits of our string. The message could potentially take the whole image so this array must be large enough to hold three two bit pairs of data for each pixel (one for the red, one for the blue, and one for the green values) after the insert point in the image 3. Most of the time the skip values and the length of the encoded message will mean that this array will never be fully used.
Once the member and local variables have been initialized we begin to decode our data from the image 4. When decoding each value we will use the opposite byte manipulation techniques to retrieve the data. For example, if the red value for the pixel is 11010010 then we just want the last two bits (the 10 value. We also need to use those values to figure out how many pixels to skip before reading the next pixel 5.
We want to parse the image until we get to our terminator character. However, we can’t determine if we have reached the terminator character until we decode the message string. We want to avoid decoding the entire image since that would be slow with larger images. The solution is to decode the bits one chunk at a time6 and see if those bits contain our terminator character 7. Once the terminator character has been reached we can return the character we have decoded as the message.
Decoding the bits from the pixels is only half of the operation. We must also convert those bits into characters. Let’s take a look at a simplified version of the decodeString method which is responsible for that conversion.
private static String decodeString(byte[] twoBitData, int start, int end)
{
StringBuffer message = new StringBuffer();
int twoBitCount = start;
for (int i = start; i < end; i += 4) {1
byte element = (byte) twoBitData[twoBitCount++];
element = (byte) (element | (twoBitData[twoBitCount++] << 2));2
element = (byte) (element | (twoBitData[twoBitCount++] << 4));
element = (byte) (element | (twoBitData[twoBitCount++] << 6));
if (element == '~') {3
m_startCharCount++;
continue;
}
if (m_startCharCount < 3) {4
return null;
}
if (element == '!') {5
m_foundTerminator = true;
break;
}
message.append((char)(element));6
}
return message.toString();
}
|
The decodeString method will read only the part of the data between start and end values. This allows the getMessage method to call this method repeatedly for different portions of the image data.
The first step is to iterate through the image data. Each character is made up of 8 bits (four two bit pairs). This loop will read four two bit pairs at a time 1 to create one character. Once we have the two bit pair from the image data we will use a binary shift and a binary OR 2 to combine that data into the value for the character.
For example, when we decode the first character in our message (capital H) the first value from the pixel will look like 00000000. We are only interested in the last two bits of this value so we used a mask to hide the rest of the data. The second pixel value will be 00000010. In this value the last two bits represent bits five and six of our character value. We will extract those bits, shift them by two and then use a binary OR to combine the value with the first byte to get the byte 00001000. The third pixel value will be 00000000. This value will get shifted four times and combined with the first and second value to create the byte 00001000. The fourth value will be 00000001. This value will be shifted six times and ORed with the value to create the final byte of 01001000 which is the ASCII byte value for a capital H.
When we encoded the string we padded it with some special characters so we would know when it started and when it stopped. The first step is to make sure that we find those start characters 3. If we don’t find the start characters then we know the image did not contain an encoded message. The start characters are important, but they are not part of the message so we need to make sure they aren’t included in the message value 4. We also need to find our terminator character and make sure we don’t include that one either 5. When we find the terminator character we know the message is done. Once we have determined that the character is not one of the start characters or the terminator character then we will just append it to our decoded message 6.
Some Notes About Binary Arithmetic
One of my good friends has been programming professionally for much longer than I have. She began her career working in assembly language. Assembly language is a very low level language where the programmer gives the computer very direct instructions in a language it can understand. Because computers use binary, every instruction must be reduced from base-10 to base-2. The large amount of time assembly language programmers spend working in base-2 made types of binary operations described in the previous sections second nature.
The C and C++ programming languages abstracted away much of the tedium of Assembly language, but it was still common to perform direct binary operations. Languages like Java, Python, and Ruby abstract the need for binary arithmetic to such a great extent that it is common to talk to professional programmers with very little experience with binary operations. This example can serve as useful introduction to binary arithmetic. There are many books and articles which provide a more complete introduction to this subject. I encourage you to find them if you are interested in learning more.
What About Unicode?
Java represents each character in memory using two bytes (16 bits). This is enough information to store the characters from languages with large alphabets like Chinese and Japanese. This method is known as Unicode or UTF-16. Most characters in the English alphabet can be encoded using just one byte (8 bits). Reserving the extra space will make English programs slightly larger, but make internationalization of applications much easier.
This sample will only support single byte characters using the ISO-8859-1 encoding. This makes our application run faster and requires half as many changes to the image when encoding the message. However, this will cause any international characters to be corrupted in the encoding and decoding process. If you are interested in encoding characters using character sets other than the English alphabet you can change the encoding and decoding methods to treat each character as two bytes instead of one.
Why Does This Program Only Save PNG Files?
When Java parses an image it will represent it in memory completely separate from the format of the file the image was saved in. This program takes that in-memory representation of the image and saves it as a PNG file. JPEG, GIF, and PNG are the three most popular formats for images on the world wide web. They are popular because they use compression to make large images take up less space and download faster. The compression used in JPEG and GIF images will corrupt the encoded message. It is possible to create a program which will generate a JPEG or GIF image, but it would require changes to the image encoding and decoding algorithms.
Conclusion
This sample is a working implementation of steganography. It provides a round-trip process by which a message can be encoded in an image and then decoded at a later point. This sample is also a a good introduction to the Java 2D API and binary arithmetic. You can use this sample in combination with an encryption program like PGP to send message with a reasonable degree of security and secrecy.
