
On a rainy Sunday afternoon my wife Mary, my daughter Audra, and I were playing inside. Audra was amusing herself with her new marble run toy. The idea is simple: you create a series of tracks and then drop a marble in the top of the toy and watch it fall down. Children love them and at two years we had just stopped worrying that Audra would eat the marbles.
The marble run delighted Audra, but it also frustrated her because she wasn’t tall enough to put the marbles in the top of the track. Mary and I looked at the situation and thought there must be a configuration that uses all of the pieces and is as short as possible. This configuration would give Audra the maximum pleasure watching the marbles go down the track. It would also be short enough that she could reach the top.
Mary and I set out to prove the best possible marble run configuration. Yes, as I’ve mentioned before, we are both engineers.
The Problem
Define a track such that the following conditions are all true:
1. Every interesting piece is used. The interesting pieces are the 1 red funnel, the 1 red foot (where the marbles end up), the 2 yellow spirals, the 3 orange cross pieces, and the 3 purple cross pieces. We need to make sure that a marble will travel through each of these pieces.

2. All paths lead through the funnel (Audra loves the funnel most of all).

3. The track is the minimum height possible. We can measure the height of the track in rows. Each blue spacer piece is one row tall. For example, the configuration at the top of this article is 15 rows tall.
Got it?
Make It Simple
Let’s start by simplifying the problem. The red funnel is two rows tall. If you add the foot underneath it then you have three rows. We have to make all paths lead through the funnel and we must have the foot at the end. QED: the configuration must be at least 3 rows tall.

That also takes care of 2 of the interesting pieces we must use. Now we are ready to begin the hard part.
Basic Understanding
If there were just cross pieces the problem would be simple. We could create a square shape and lay the cross pieces in a criss-cross pattern. This is because each cross piece (the purple and orange pieces differ only in color) spans 1 row and takes up 2 spaces in that row. It takes 1 space for the entrance and another space for the exit.
The yellow spirals make it complicated. Each yellow spiral spans 3 rows and takes up 1 space per row. There is 1 space for the entrance, 1 space for the exit, and 1 space just above the exit. The spirals are tight enough that putting a piece right above the exit blocks the marble on the spiral.
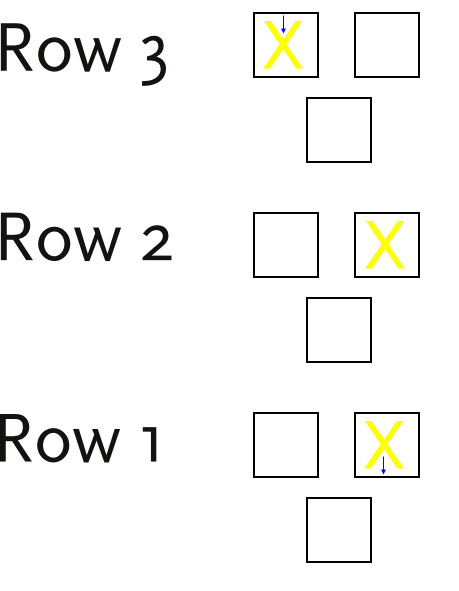
Combine The Spirals
Each spiral takes 3 rows. Putting them on top of each other would make 6 rows. Not very efficient. The first thing we tried is combining spirals. 2 spirals take up 6 spaces over at least 3 rows. It seems like you can gain an advantage by combining the 2 spirals into 3 rows, but you can’t.
If both spirals have their entrances on the same row then you can’t feed the marbles into them. Each cross piece takes up 2 of the 3 spaces so you can’t have two entrances on the same row without adding extra spacer and ending up with an extra row. QED: combining the 2 spirals together must use 4 rows.
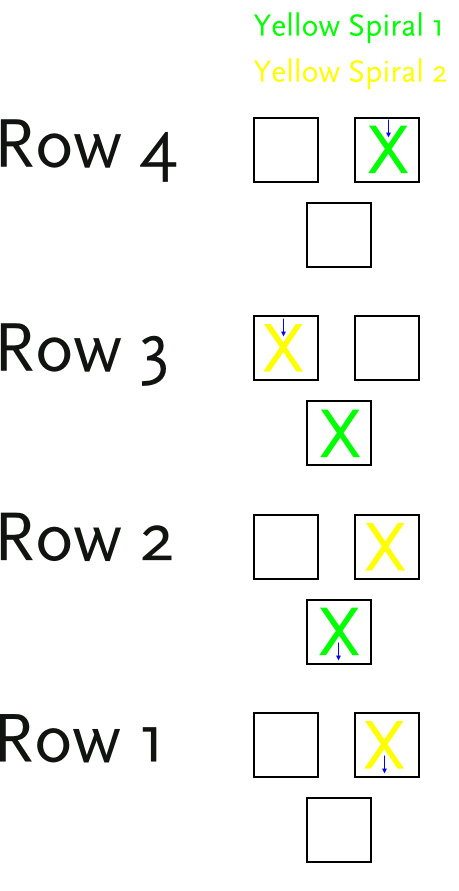
Within those 4 rows we can add two cross pieces: one after spiral 1 and the other before spiral 2.
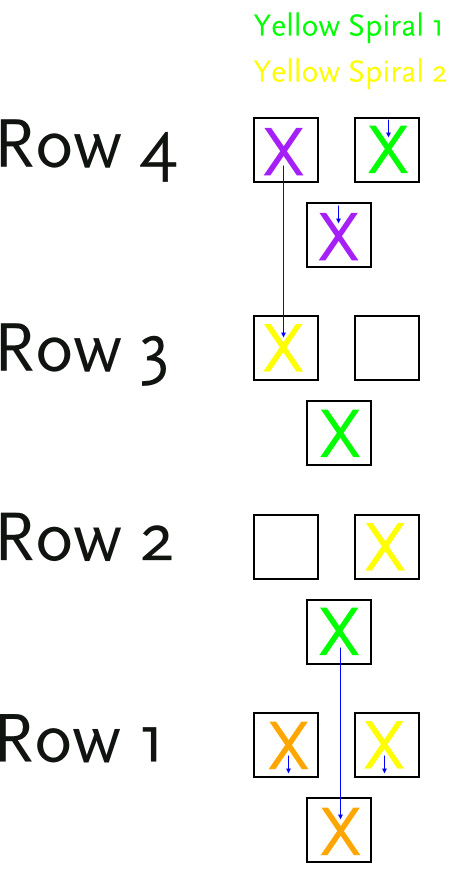
This is pretty good. Mary and I used up 4 total pieces in 4 rows with 2 spaces remaining. We can combine everything together and get 11 rows.

That isn’t bad, but I thought we could make it better.
Separate The Spirals
When we put the spirals together we have 4 cross pieces left over. Each one of those pieces takes up 2 of the 3 available spaces in a row. That isn’t very efficient. We needed a way to fill those unused spaces. The solution was separating the spirals.
If you separate the spirals you can combine 1 spiral with 3 cross pieces. This takes up every available space and makes the configuration perfect.
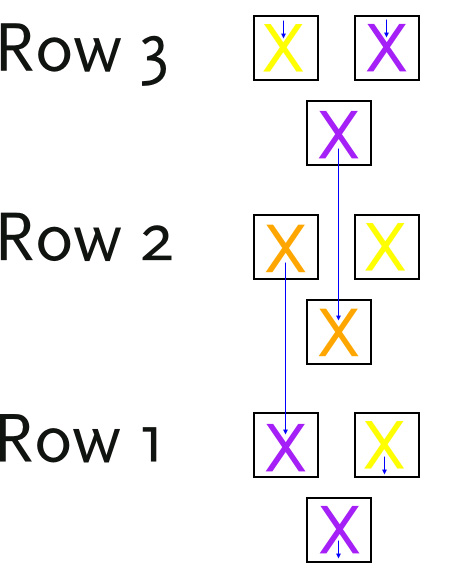

The Perfect Combination
Is it perfect? We are using every available space. That is a pretty good indication that we are as efficient as possible, but it isn’t certain. Want more proof? That takes some logic:
- We know that a cross piece must take 2 of the available spaces on each row.
- We also know that a yellow spiral is 3 rows tall and takes one space from each row.
- That means a cross piece and a yellow spiral one one level will always be an odd number. Add as many cross pieces as you want it will still be an odd number.
- We know the number of rows can’t be 1 because that leaves no room for any cross pieces.
- It also can’t be 2 because it must be an odd number.
- Therefore 3 is the smallest number of columns that works and a configuration that takes up every available space must be the most efficient.
This leave one more question. What about adding more columns? We can put the two 3 row sections next to each other and make a structure with 6 columns. That configuration is only 6 rows tall. However, that fails to meet requirement 1 since you can’t have the marble go through every piece.
QED: 3 row tall separate spirals is the most efficient configuration.

And now we have the perfect combination (we think). Audra is happy because, at 9 rows tall, she can reach the top. Her parents are happy too. We got to geek out a little bit and be caring parents at the same time.
See any errors with our logic? Is it possible to make it less than 9 rows? I’d love to hear your solution.